上一点，且∠AED=45°。
（1）判断CD与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为6cm，AE=10cm，求∠ADE的正弦值。
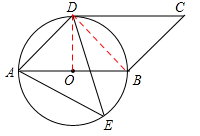
【答案】解：（1）连接BD，OD，
∵AB是直径，∴∠ADB=90°。
∵∠ABD=∠E=45°，∴∠DAB=45°，则AD=BD。
∴△ABD是等腰直角三角形。∴OD⊥AB。
又∵DC∥AB，∴OD⊥DC，∴CD与⊙O相切。
（2）过点O作OF⊥AE，连接OE，
则AF=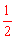
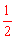AE=×10=5。
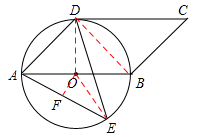
∵OA=OE，∴∠AOF=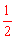∠AOE。
∵∠ADE=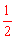∠AOE，∴∠ADE=∠AOF。
在Rt△AOF中，sin∠AOF=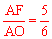
，
∴sin∠ADE= sin∠AOF =。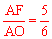
【考点】平行四边形的性质，圆周角定理，等腰直角三角形的判定和性质，切线的判定，垂径定理，锐角三角函数定义。
【分析】（1）连接OD，BD，由AB为直径，∠AED=45°，证得△ABD是等腰直角三角形，即AD=BD，
然后由等腰三角形的性质，可得OD⊥AB，又由四边形ABCD是平行四边形，即可证得OD⊥CD，即可
证得CD与⊙O相切。
（2）过点O作OF⊥AE，连接OE，由垂径定理可得AF=6，∠AOF=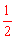∠AOE，又由圆周角定理
可得∠ADE=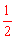∠AOE，从而证得∠AOF=∠ADE，然后在Rt△AOF中，求得sin∠AOF的值，即可求得答案。
11.（2012四川资阳9分）如图，在△ABC中，AB＝AC，∠A＝30°，以AB为直径的⊙O交BＣ于点D，交AC于点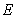
，连结DE，过点B作BP平行于DE，交⊙O于点P，连结EP、CP、OP．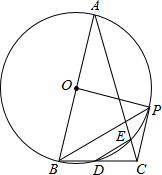
（1）(3分)BD＝DC吗？说明理由；
（2）(3分)求∠BOP的度数；
（3）(3分)求证：CP是⊙O的切线；
如果你解答这个问题有困难，可以参考如下信息：
为了解答这个问题，小明和小强做了认真的探究，然后分别用不同的思路完成了这个题目．在进行小组交流的时候，小明说：“设OP交AC于点G，证△AOG∽△CPG”；小强说：“过点C作CH⊥AB于点H，证四边形CHOP是矩形”．
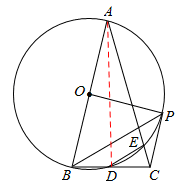【答案】解：（1）BD=DC。理由如下：连接AD，
∵AB是直径，∴∠ADB=90°。
∵AB=AC，∴BD=DC。
（2）∵AD是等腰△ABC底边上的中线，
∴∠BAD=∠CAD 。∴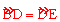
。
∴BD=DE。
∴BD=DE=DC。∴∠DEC=∠DCE。
∵△ABC中，AB=AC，∠A=30°，
∴∠DCE=∠ABC=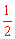
(180°－30°)=75°。∴∠DEC=75°。
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] 下一页
- 圆形练习题及答案（七）
- › 圆形练习题及答案（十）
- › 圆形练习题及答案（五）
- › 圆形练习题及答案（六）
- › 圆形练习题及答案（七）
- › 圆形练习题及答案（八）
- › 圆形练习题及答案汇总
- 在百度中搜索相关文章：圆形练习题及答案（七）
- 在谷歌中搜索相关文章：圆形练习题及答案（七）
- 在soso中搜索相关文章：圆形练习题及答案（七）
- 在搜狗中搜索相关文章：圆形练习题及答案（七）