,点P满足
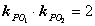
(1)求动点P的轨迹方程;
(2)过点Q(1,2)能否做直 线AB与P的轨迹交于A、B两点,并且使Q是AB的中点?如果存在,求出直线AB的方程;若不存在,请说明理由。
线AB与P的轨迹交于A、B两点,并且使Q是AB的中点?如果存在,求出直线AB的方程;若不存在,请说明理由。
16.(本题满分11分)
某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
第二部分 能力检测(共50分)
四、填空题:本大题共2小题,每小题5分,共1 0分.
0分.
17.若在曲线f(x,y)=0上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”。下列方程:①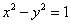 ;②
;②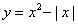 ;③
;③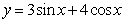 ;④
;④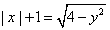 对应的曲线中存在“自公切线”的有_____________.
对应的曲线中存在“自公切线”的有_____________.
 18.如图,已知椭圆
18.如图,已知椭圆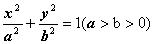 ,O为
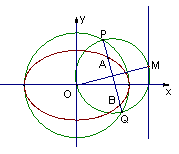
,O为 原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是___________.
原点,点M是椭圆右准线上的动点,以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点,直线PQ与椭圆相交于A、B两点,则|AB|的取值范围是___________.
五、解答题:本大题共3小题,共40分.解答应写出文字说明、证明过程或演算步骤.
19.(本题满分12分)
已知圆C:(x-1)2+(y+2)2=9,直线l:(m+1)x-y-2m-3=0(m∈R)
(1)求证:无论m取什么实数,直线恒与圆交于两点;
(2)求直线l被圆C所截得的弦长最小时的直线方程.
20.(本题满分13分)
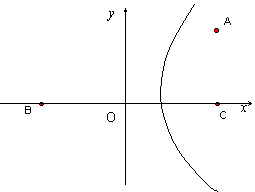 A村在C村正北
A村在C村正北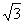 km处,B地在C村正西16km处,已知弧形公路PQ上任一点到B、C两点的距离之差为8km.
km处,B地在C村正西16km处,已知弧形公路PQ上任一点到B、C两点的距离之差为8km.
(1)如图,以BC中点O为原点,建立坐标系,求弧形公路PQ所在曲线的方程;
(2)现要在公路旁建造一个变电站M分别向A村、C村送电,但A村有一村办工厂用电需用专用线路, 不得与民用混线用电,因此向A村要架两条线路分别给村民和工厂送电. 要使用电线最短,变电站M应建在A村的什么方位,并求出M到A村的距离.
不得与民用混线用电,因此向A村要架两条线路分别给村民和工厂送电. 要使用电线最短,变电站M应建在A村的什么方位,并求出M到A村的距离.
21.(本题满分15分)
点P到x轴的距离比它到点(0,1)的距离小1,称点P的轨迹为曲线C,点M为直线l:y=-m (m>0)上任意一点,过点M作曲线C的两条切线MA,MB,切点分别为A,B.
(1)求曲线C的轨迹方程;
(2)当M的坐标为(0,-l)时,求过M, A,B三点的圆的标准方程,并判断直线l与此圆的位置关系;
A,B三点的圆的标准方程,并判断直线l与此圆的位置关系;
(3)当m变化时,试探究直线l上是否存在点M,使MA ⊥MB?若存在,有几个这样的点,若不存在,请说明理由。
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页
- 广东实验中学高二上册数学理科试卷及答案
- › 广东实验中学高二上册英语期末试卷及答案
- › 广东实验中学高二上册数学文科试卷及答案
- › 广东实验中学高二上册数学理科试卷及答案
- › 广东实验中学高一上册数学期末试卷及答案
- 在百度中搜索相关文章:广东实验中学高二上册数学理科试卷及答案
- 在谷歌中搜索相关文章:广东实验中学高二上册数学理科试卷及答案
- 在soso中搜索相关文章:广东实验中学高二上册数学理科试卷及答案
- 在搜狗中搜索相关文章:广东实验中学高二上册数学理科试卷及答案
