
一、选择题:(每题5分,共60分)
1.若复数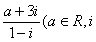 是虚数单位)是纯虚数,则实数a的值为( )
是虚数单位)是纯虚数,则实数a的值为( )
A.-3 B.3 C.-6 D.6
2.用反证法证明:若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a、b、c中至少有一个是偶数.用反证法证明时,下列假设正确的是( )
A.假设a、b、c都是偶数 B.假设a、b、c都不是偶数
C.假设a、b、c至多有一个偶数 D.假设a、b、c至多有两个偶数
3.分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0”,求证“√(b2-ac)﹤√(3a)”索的因应是( )
A.a-b>0 B.a-c>0 C.(a-b)(a-c)>0 D.(a-b)(a-c)<04.
4.给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复 数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b=c+d⇒a=c,b=d”;
数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b=c+d⇒a=c,b=d”;
③若“a,b∈R,则a-b>0⇒a>b”类比推出“若a,b∈C,则a-b>0⇒a>b”.
其中类比结论正确 的个数是( )
的个数是( )
A.0 B.1 C.2 D.3
5.推理“①矩形是平行四边形;②三角形不是平行四边形;③三角形不是矩形”中的小前提是( )
A.① B.② C.③ D.①和②
6.复数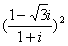 ( )
( )
A.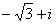 B.
B.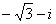 C.
C.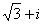 D.
D.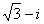
7.函数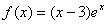 的单调递增区间是( )
的单调递增区间是( )
A.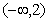 B.(0,3) C.(1,4) D.
B.(0,3) C.(1,4) D.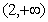
8.抛物线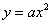 的焦点坐标是( )
的焦点坐标是( )
A.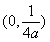 B.
B. C.
C.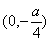 D.
D.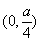
9.设双曲 线
线 的虚轴长为2,焦距为
的虚轴长为2,焦距为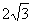 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.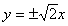 B.
B.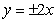 C.
C.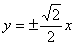 D.
D.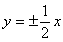
10.设函数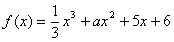 在区间[1,3]上是单调函数,则实数a的取值范围是( )
在区间[1,3]上是单调函数,则实数a的取值范围是( )
A.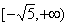 B.
B.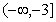 C.
C.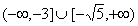 D.
D.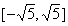
11.为了表示 个点与相应直线在整体上的接近程度,我们常用( )表示
个点与相应直线在整体上的接近程度,我们常用( )表示
A.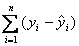 B.
B.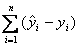 C.
C.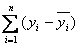 D.
D.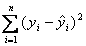
12. 过双曲线 的左焦点
的左焦点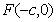 作圆
作圆 的切线,切点为E,延长FE交抛物线
的切线,切点为E,延长FE交抛物线 于点P,若E为线段FP的中点,则双曲线的离心率为( )
于点P,若E为线段FP的中点,则双曲线的离心率为( )
A.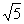 B.
B.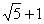 C.
C.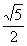 D.
D.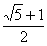
二、填空题:(每题5分,共20分)
13.双曲线 的一个焦点是
的一个焦点是 ,
, 则m的值是_________.
则m的值是_________.
14.曲线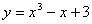 在点(1,3)处的切线方程为___________________.
在点(1,3)处的切线方程为___________________.
15.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是_____________.
16.设n为正整数,f(n)=1+1/2+1/3+…+1/n,计算得f(2)=3/2,f(4)>2,f(8)>5/2,f(16) >3,观察上述结果,可推测一般的结论为_______________________________.
>3,观察上述结果,可推测一般的结论为_______________________________.
三、解答题:
17.(本题满分12分)
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.
(1)求抛物线C的标准方程;
(2)设直线l是抛物线的准线,求证:以AB为直径的圆与准线l相切.
www.kuaixue5.com18.(本题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 |
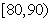 |
 |
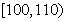 |
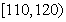 |
 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
乙班
| 成绩 |
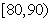 |
 |
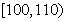 |
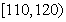 |
 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
(1)现从甲班成绩位于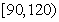 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;
(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下,“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由。
| 成绩小于100分 | 成绩不小于100分 | 合计 | |
| 甲班 |
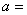 |
26 | 50 |
| 乙班 | 12 |
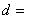 |
50 |
| 合计 | 36 | 64 | 100 |
附:
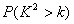 |
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
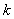 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.(本题满分12分)
已知函数 ,其图象在点(1,
,其图象在点(1,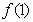 )处的切线方程为
)处的切线方程为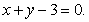
(1)求a,b的值;
(2)求函数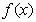 的单调区间,并求出
的单调区间,并求出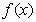 在区间[—2,4]上的最大值。
在区间[—2,4]上的最大值。
20.(本题满分12分)
已知椭圆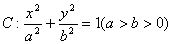 的离心率为
的离心率为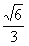 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
(1)求椭圆C的方程;
(2)设直线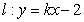 与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线
与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线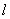 的方程
的方程 。
。
21.(本题满分 12分)已知函数
12分)已知函数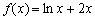 ,
,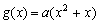
(1)若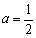 ,求
,求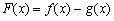 的单调区间;
的单调区间;
(2)当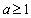 时,求证:
时,求证: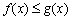 .
.
22.(本题满分12分)
某市旅游部门开发一种旅 游纪念品,每件产品的成本是
游纪念品,每件产品的成本是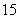 元,销售价是
元,销售价是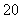 元,月平均销售
元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术
件.通过改进工艺,产品的成本不变,质量和技术 含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为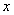
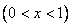 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为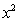 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是 (元).
(元).
(1)写出 与
与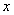 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
参考答案:
一.选择题:BBCCB ADACC DD
二.填空题:13,-2; 14,2x-y+1=0; 15。Y=1.23x+0.08;16,f( )≥
)≥
三.解答题:

18.(1)用分层抽样的方法更合理;在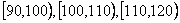 ,各分数段抽取4份,3份,2份试卷。
,各分数段抽取4份,3份,2份试卷。
(2)估计乙班的平均分数为
105.8-101。8=4,即两班的平均分数差4分。
(3)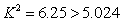
所以,在犯错误的概率不超过0。025的前提下,认为两个班的成绩有差异。
19.J解:(1)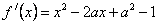 ,由题意得。
,由题意得。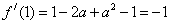 得:A=-1 b=
得:A=-1 b=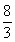
(2) 得:x=1或x=0,有列表得,
得:x=1或x=0,有列表得,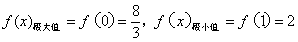
而f(-2)=-4,f(4)=8,所以,f(x)的最大值为8
20.解:(I)由已知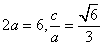 ,解得
,解得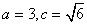
所以椭圆C的方程为

21.解:(1) ,
,
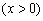
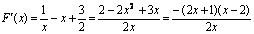
∵ ,∴当
,∴当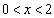 时,
时,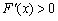 ,当
,当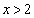 时,
时,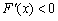 ,
,
∴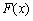 的增区间为
的增区间为 ,
, 减区间为
减区间为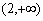
(2)令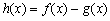
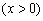
则由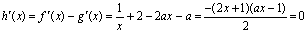 解得
解得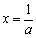
∵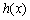 在
在 上增,在
上增,在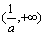 上减
上减
∴当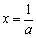 时,
时,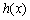 有最小值,
有最小值,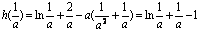
∵ ,∴
,∴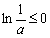 ,
,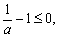
∴ ,所以
,所以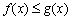
22.解:(Ⅰ)改进工艺后,每件产品的销 售价为
售价为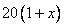 ,月平均销售量为
,月平均销售量为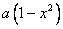 件,则月平均利润
件,则月平均利润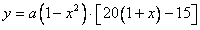 (元),
(元),
∴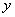 与
与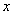 的函数关系式为
的函数关系式为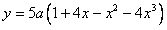

(Ⅱ)由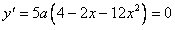 得
得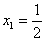 ,
,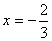 (舍)
(舍)
当 时
时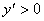 ;
;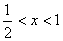 时
时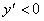 ,∴函数
,∴函数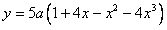
 在
在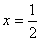 取得最大值.
取得最大值.
故改进工艺后,产品的销售价为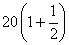
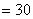 元时,旅游部门销售该纪念品的月平均利润最大.
元时,旅游部门销售该纪念品的月平均利润最大.
- 银川一中高二上册数学文科试卷及答案
- › 宁夏银川一中高考语文二模试卷及答案
- › 银川一中高二上册数学文科试卷及答案
- › 宁夏银川一中高二语文期中试卷及答案
- › 银川一中高一上册英语期末试卷及答案
- 在百度中搜索相关文章:银川一中高二上册数学文科试卷及答案
- 在谷歌中搜索相关文章:银川一中高二上册数学文科试卷及答案
- 在soso中搜索相关文章:银川一中高二上册数学文科试卷及答案
- 在搜狗中搜索相关文章:银川一中高二上册数学文科试卷及答案
