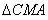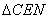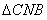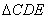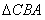∽
，
∽
，
∽
.
于是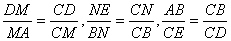
.
由切线长定理知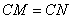
，
所以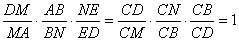
，
于是由塞瓦定理可知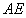
、
、
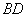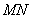相交于点P.
又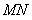
⊥
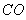，所以
，
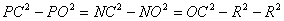即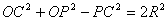
.
二、证明：设分为三个集合A、B、C.
假设A中无距离为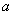
的点，B中无距离为
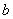的点， C中无距离为
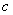的点。
不妨设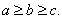
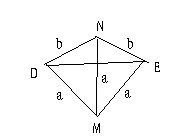从A中任取一点M，以M为球心作半径为
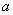的球面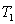
，该球面上的点属于B或C，若这些点全在C中，则其中必有2点距离为
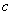，矛盾！故该球面上有一点N
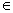B，以N为球心，
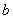为半径的球面
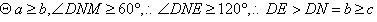与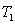
上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页
Tag:高二数学辅导，高二数学辅导资料，高中学习 - 高二学习 - 高二数学 - 高二数学辅导
- 2017高二竞赛班数学暑假作业答案(五)
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高二竞赛班数学暑假作业答案(五)
- 在谷歌中搜索相关文章：2017高二竞赛班数学暑假作业答案(五)
- 在soso中搜索相关文章：2017高二竞赛班数学暑假作业答案(五)
- 在搜狗中搜索相关文章：2017高二竞赛班数学暑假作业答案(五)