又∵∠DAB=∠BCD,∴∠EAF=∠FCE.
∴四边形EAFC是平行四边形.
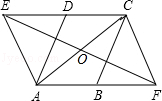
点评:本题考查了等边三角形的性质及平行四边形的判定.多种知识综合运用是解题中经常要遇到的.
七、(12分)
25.考点:反比例函数综合题.
分析:(1)先把(a,b)、(a+2,b+k)代入y=2x+1得到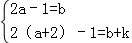 ,然后结果代数式变形可解得k=4,则可确定反比例函数解析式;
,然后结果代数式变形可解得k=4,则可确定反比例函数解析式;
(2)把一次函数与反比例函数解析式组成方程组,再解方程组可确定A点坐标;
(3)先利用勾股计算出OA=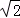 ,过A点作AP1⊥x轴,则△OAP1为等腰三角形;作点O关于AP1的对称点P2,则△OAP2为等腰三角形;以O点为圆心,OA为半径画弧交x轴与P3,P4,则△OAP3、△OAP4为等腰三角形;然后利用线段长分别确定各点坐标.
,过A点作AP1⊥x轴,则△OAP1为等腰三角形;作点O关于AP1的对称点P2,则△OAP2为等腰三角形;以O点为圆心,OA为半径画弧交x轴与P3,P4,则△OAP3、△OAP4为等腰三角形;然后利用线段长分别确定各点坐标.
解答:解:(1)把(a,b)、(a+2,b+k)代入y=2x+1得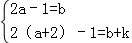 ,解得k=4,
,解得k=4,
所以反比例函数解析式为y= ;
;
(2)解方程组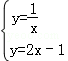 得
得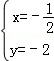 或
或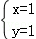 ,
,
∵A点在第一象限,
∴点A的坐标为(1,1);
(3)存在.
OA=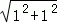 =
=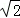 ,
,
满足条件的点P坐标为( 1,0)、(2,0)、(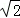 ,0)、(﹣
,0)、(﹣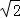 ,0).
,0).

点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰三角形的判定与性质;运用分类讨论的思想解决问题.
八、(14分)
26.考点:等腰梯形的性质;一元二次方程的应用.
专题:压轴题;开放型.
分析:(1)先作AK⊥BC于K,FG⊥BC于G,根据等腰梯形的性质,可得BK= (BC﹣AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=
(BC﹣AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=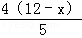 ,利用面积公式可得S△BEF=﹣
,利用面积公式可得S△BEF=﹣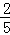 x2+
x2+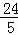 x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);(2)根据题意,结合(1)中面积的表达式,可以得到
x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);(2)根据题意,结合(1)中面积的表达式,可以得到
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] 下一页
- 初三上册数学期末试卷及答案(人教版)
- › 初三上册语文期末复习训练
- › 初三上册语文常考简答题、默写题
- › 初三上册英语第一单元试卷答案
- › 初三上册英语第二单元试卷
- › 初三上册英语第二单元试卷答案
- › 初三上册英语第三单元试卷及答案
- › 初三上册英语第四单元试卷及答案
- › 初三上册英语第五单元试卷及答案
- › 初三上册英语第六单元试卷及答案
- › 初三上册英语第七单元试卷及答案
- › 初三上册英语第九单元试卷及答案
- › 2016学年度初三上册语文入学测试答案
- 在百度中搜索相关文章:初三上册数学期末试卷及答案(人教版)
- 在谷歌中搜索相关文章:初三上册数学期末试卷及答案(人教版)
- 在soso中搜索相关文章:初三上册数学期末试卷及答案(人教版)
- 在搜狗中搜索相关文章:初三上册数学期末试卷及答案(人教版)
