∴x=3﹣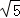 ,y=3+
,y=3+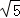 ,即A(3﹣
,即A(3﹣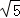 ,3+
,3+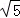 ),
),
∴矩形的面积=(3﹣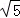 )(3+
)(3+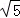 )=4;
)=4;
矩形的周长=2(3﹣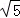 )+2(3+
)+2(3+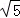 )=12.
)=12.
故选A.
点评:本题考查的是一次函数与反比例函数的交点问题,根据题意得出关于x、y的方程组是解答此题的关键.
6.考点:反比例函数图象上点的坐标特征.
分析:根据反比例函数的比例系数的符号可得反比例函数所在象限为二、四,其中在第四象限的点的纵坐标总小于在第二象限的纵坐标,进而判断在同一象限内的点B和点C的纵坐标的大小即可.
解答:解:∵反比例函数的比例系数为﹣1,
∴图象的两个分支在二、四象限;
∵第四象限的点的纵坐标总小于在第二象限的纵坐标,点A在第二象限,点B、C在第四象限,
∴y1最大,
∵1> ,y随x的增大而增大,
,y随x的增大而增大,
∴y2>y3,
∴y1>y2>y3
故选A.
点评:考查反比例函数图象上点的坐标特征;用到的知识点为:反比例函数的比例系数小于0,图象的2个分支在二、四象限;第四象限的点的纵坐标总小于在第二象限的纵坐标;在同一象限内,y随x的增大而增大.
7.考点:线段垂直平分线的性质.
专题:应用题.
分析:为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
解答:解:利用线段垂直平分线的性质得:要放在三边中垂线的交点上.
故选D.
点评:本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.
8.考点:勾股定理;翻折变换(折叠问题).
专题:压轴题.
分析:根据折叠的性质,只要求出DN就可以求出NE,在直角△CEN中,若设CN=x,则DN=NE=8﹣x,CE=4cm,根据勾股定理就可以列出方程,从而解出CN的长.
解答:解:设CN=xcm,则DN=(8﹣x)cm,由折叠的性质知EN=DN=(8﹣x)cm,
而EC= BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2,即(8﹣x)2=16+x2,
BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2,即(8﹣x)2=16+x2,
整理得16x=48,所以x=3.
故选A.
点评:折叠问题其实质是轴对称,对应线段相等,对应角相等,通常用勾股定理解决折叠问题.
二、认真填一填:(本大题共8小题,每小题3分,共24分.)
9.13考点:一元二次方程的解.
分析:把x= 代入关于x的方程x2﹣6x+a=0,列出关于a的方程,通过解该方程来求得a的值,然后把a的值代入所求的代数式并求值即可.
代入关于x的方程x2﹣6x+a=0,列出关于a的方程,通过解该方程来求得a的值,然后把a的值代入所求的代数式并求值即可.
解答:解:由题意,得(3﹣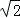 )2﹣6(3﹣
)2﹣6(3﹣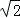 )+a=0,即﹣7+a=0,
)+a=0,即﹣7+a=0,
解得a=7,则2a﹣1=2×7﹣1=13.
故答案是:13.
点评:本题主要考查了方程的解的定义.方程的根即方程的解,就是能使方程左右两边相等的未知数的值. 10.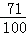
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] 下一页
- 初三上册数学期末试卷及答案(人教版)
- › 初三上册语文期末复习训练
- › 初三上册语文常考简答题、默写题
- › 初三上册英语第一单元试卷答案
- › 初三上册英语第二单元试卷
- › 初三上册英语第二单元试卷答案
- › 初三上册英语第三单元试卷及答案
- › 初三上册英语第四单元试卷及答案
- › 初三上册英语第五单元试卷及答案
- › 初三上册英语第六单元试卷及答案
- › 初三上册英语第七单元试卷及答案
- › 初三上册英语第九单元试卷及答案
- › 2016学年度初三上册语文入学测试答案
- 在百度中搜索相关文章:初三上册数学期末试卷及答案(人教版)
- 在谷歌中搜索相关文章:初三上册数学期末试卷及答案(人教版)
- 在soso中搜索相关文章:初三上册数学期末试卷及答案(人教版)
- 在搜狗中搜索相关文章:初三上册数学期末试卷及答案(人教版)
