考点：概率公式．
专题：计算题．
分析：根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数．二者的比值就是其发生的概率的大小．
解答：解：由题意知：3000人中有2130人看中央电视台的《焦点访谈》，
∴在该县随便问一个人，他看《焦点访谈》的概率大约是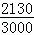
=
．
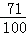故答案为：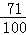
．
点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=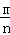
．
11．18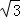
考点：菱形的性质．
分析：根据菱形对角线垂直且互相平分，且每条对角线平分它们的夹角，即可得出菱形的另一一条对角线长，再利用菱形的面积公式求出即可．
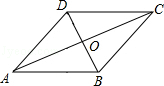
解答：解：如图所示：∵菱形有一个内角为60°，较短的对角线长为6，
∴设∠BAD=60°，BD=6，
∵四边形ABCD是菱形，
∴∠BAC=∠DAC=30°，DO=BO=3，
∴AO=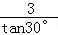
=3，
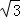∴AC=6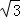，则它的面积为：
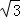×6×6=18．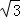
故答案为：18．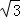
点评：此题主要考查了菱形的性质，熟练掌握菱形的面积公式以及对角线之间的关系是解题关键．
12．矩形考点：矩形的判定；平行线的性质；三角形中位线定理；平行四边形的判定；菱形的性质．
专题：证明题．
分析：连接AC、BD交于O，根据三角形的中位线定理推出EF∥BD∥HG，EH∥AC∥FG，得出四边形EFGH是平行四边形，根据菱形性质推出AC⊥BD，推出EF⊥EH，即可得出答案．
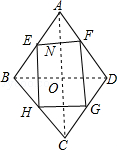解答：解：连接AC、BD交于O，
∵E、F、G、H分别是AB、AD、CD、BC的中点，
∴EF∥BD，FG∥AC，HG∥BD，EH∥AC，
∴EF∥HG，EH∥FG，
∴四边形EFGH是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
∵EF∥BD，EH∥AC，
∴EF⊥EH，
∴∠FEH=90°，
∴平行四边形EFGH是矩形，
故答案为：矩形．
点评：本题考查了矩形的判定，菱形的性质，平行四边形的判定，平行线性质等知识点的运用，主要考查学生能否正确运用性质进行推理，题目比较典型，难度适中．
13．空心的圆柱考点：由三视图判断几何体．
分析：两个视图是矩形，一个视图是个圆环，那么符合这样条件的几何体是空心圆柱．
解答：解：如图，该几何体的三视图中两个视图是矩形，一个视图是个圆环，故该几何体为空心圆柱．
点评：本题考查由三视图确定几何体的形状，主要考查学生空间想象能力及对立体图形的认知能力．
14．（x+2）2﹣100 ．考点：配方法的应用．
专题：计算题．
分析：前两项加上4再减去4变形，利用完全平方公式化简即可得到结果．
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] 下一页
- 初三上册数学期末试卷及答案（人教版）
- › 初三上册语文期末复习训练
- › 初三上册语文常考简答题、默写题
- › 初三上册英语第一单元试卷答案
- › 初三上册英语第二单元试卷
- › 初三上册英语第二单元试卷答案
- › 初三上册英语第三单元试卷及答案
- › 初三上册英语第四单元试卷及答案
- › 初三上册英语第五单元试卷及答案
- › 初三上册英语第六单元试卷及答案
- › 初三上册英语第七单元试卷及答案
- › 初三上册英语第九单元试卷及答案
- › 2016学年度初三上册语文入学测试答案
- 在百度中搜索相关文章：初三上册数学期末试卷及答案（人教版）
- 在谷歌中搜索相关文章：初三上册数学期末试卷及答案（人教版）
- 在soso中搜索相关文章：初三上册数学期末试卷及答案（人教版）
- 在搜狗中搜索相关文章：初三上册数学期末试卷及答案（人教版）