八、（14分）
26．（14分）（2010•鞍山）在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10．点E在下底边BC上，点F在腰AB上．
（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积；
（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；
（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1：2的两部分？若存在，求出此时BE的长；若不存在，请说明理由．
参考答案：
一、精心选一选（本大题共8小题，每小题3分，共24分）
1．考点：平行投影．
分析：解：根据平行投影的特点和规律可知，C，D是上午，A，B是下午，根据影子的长度可知先后为C→D→A→B．
解答：解：根据平行投影的特点和规律可知，C，D是上午，A，B是下午，
根据影子的长度可知先后为C→D→A→B．
故选C．
点评：本题考查平行投影的特点和规律．在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，就北半球而言，从早晨到傍晚物体的指向是：西﹣西北﹣北﹣东北﹣东，影长由长变短，再变长．
2．考点：勾股定理；解一元二次方程-因式分解法．
专题：分类讨论．
分析：求出方程的解，得出直角三角形的两边长，分为两种情况：①当3和4是两直角边时，②当4是斜边，3是直角边时，根据勾股定理求出第三边即可．
解答：解：x2﹣7x+12=0，
（x﹣3）（x﹣4）=0，
x﹣3=0，x﹣4=0，
解得：x1=3，x2=4，
即直角三角形的两边是3和4，
当3和4是两直角边时，第三边是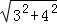
=5；
当4是斜边，3是直角边时，第三边是 
=
，
即第三边是5或，
故选D．
点评：本题考查了解一元二次方程和勾股定理，注意：解此题时要进行分类讨论．
3．考点：一元二次方程的解．
专题：计算题．
分析：一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值；即用这个数代替未知数所得式子仍然成立；将x=3代入原方程即可求得2a的值．
解答：解：把x=3代入原方程得：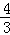
×9﹣2a+1=0，
∴2a=13；
故选C．
点评：本题考查的是一元二次方程的根即方程的解的定义．
4．考点：命题与定理．
分析：利用梯形可对A进行判断；根据平行四边形的判定方法对B进行判断；根据等腰梯形的性质对C进行判断；根据平行四边形的性质对D进行判断．
解答：解：A、直角梯形的一对邻角互补，所以A选项的命题为假命题；
B、一组对边平行，一组对角相等的四边形是平行四边形，所以B选项为真命题；
C、等腰梯形的对角线相等，所以C选项为真命题；
D、平行四边形的对角线互相平分，所以D选项为真命题．
故选A．
点评：本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．
5．考点：反比例函数与一次函数的交点问题．
专题：探究型．
分析：先根据两函数图象的交点在第一象限可知x＞0，y＞0，再根据两函数有交点可列出关于x、y的方程组，求出x，y的值，再根据矩形的面积及周长公式进行解答即可．
解答：解：∵两函数图象的交点在第一象限，
∴x＞0，y＞0，
∴
，
∴
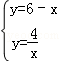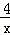=6﹣x，
∴x2﹣6x+4=0，
解得x=3±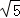
，
∵A在B的左边，
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] 下一页
- 初三上册数学期末试卷及答案（人教版）
- › 初三上册语文期末复习训练
- › 初三上册语文常考简答题、默写题
- › 初三上册英语第一单元试卷答案
- › 初三上册英语第二单元试卷
- › 初三上册英语第二单元试卷答案
- › 初三上册英语第三单元试卷及答案
- › 初三上册英语第四单元试卷及答案
- › 初三上册英语第五单元试卷及答案
- › 初三上册英语第六单元试卷及答案
- › 初三上册英语第七单元试卷及答案
- › 初三上册英语第九单元试卷及答案
- › 2016学年度初三上册语文入学测试答案
- 在百度中搜索相关文章：初三上册数学期末试卷及答案（人教版）
- 在谷歌中搜索相关文章：初三上册数学期末试卷及答案（人教版）
- 在soso中搜索相关文章：初三上册数学期末试卷及答案（人教版）
- 在搜狗中搜索相关文章：初三上册数学期末试卷及答案（人教版）