2013高考数学复习：平面向量与复数（四）
【知识图解】
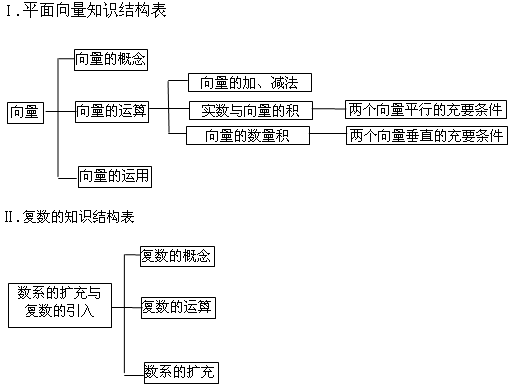
【方法点拨】
由于向量融形、数于一体，具有几何形式与代数形式的“双重身份”，使它成为了中学数学知识的一个重要交汇点，成为联系众多知识内容的媒介。所以，向量成为了“在知识网络交汇处设计试题”的很好载体。从高考新课程卷来看，对向量的考查力度在逐年加大，除了直接考查平面向量外，将向量与解析几何、向量与三角等内容相结合，在知识交汇点处命题，既是当今高考的热点，又是重点。
复习巩固相关的平面向量知识，既要注重回顾和梳理基础知识，又要注意平面向量与其他知识的综合运用，渗透用向量解决问题的思想方法，从而提高分析问题与综合运用知识解决问题的能力，站在新的高度来认识和理解向量。
【例1】向量是具有大小和和方向的量，具有“数”和“形”的特点，向量是数形结合的桥梁，在处理向量问题时注意用数形结合思想的应用.
【例2】 平面向量基本定理是处理向量问题的基础，也是平面向量坐标表示的基础，它表明同一平面内任意向量都可以表示为其他两个不共线向量的线性组合.
【例3】 向量的坐标表示实际上是向量的代数形式，引入坐标表示，可以把几何问题转化为代数问题解决.
【例4】要了解向量的工具作用，熟悉利用向量只是解决平面几何及解析几何中的简单问题的方法.
第4课 向量综合应用
【考点导读】
1. 能综合运用所学向量知识及有关数学思想方法解决向量知识内部综合问题和与函数、不等式、三角函数、数列等知识的综合问题.
2. 能从实际问题中提炼概括数学模型，了解向量知识的实际应用.
【基础练习】
1.已知a＝（5，4），b＝（3，2），则与2a－3b平行的单位向量为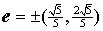
2.已知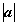
＝1，
＝1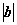，a与b的夹角为60°，x＝2a－b，y＝3b－a，则x与y的夹角的余弦值为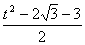
【范例导析】
例1.已知平面向量a＝(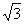
，－1)，b＝(
， 
).
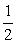(1) 若存在实数k和t，便得x＝a＋(t2－3)b， y＝－ka＋tb，且x⊥y，试求函数的关系式k＝f（t）；
(2)根据(1)的结论，确定k＝f(t)的单调区间。
分析:利用向量知识转化为函数问题求解.
解:（1）法一：由题意知x＝(，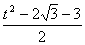
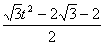)， y＝(
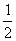t－
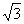k，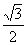
t＋k)，又x⊥y
故x·y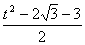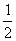＝×（t－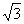
- 2017高考数学复习：平面向量与复数（四）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：平面向量与复数（四）
- 在谷歌中搜索相关文章：2017高考数学复习：平面向量与复数（四）
- 在soso中搜索相关文章：2017高考数学复习：平面向量与复数（四）
- 在搜狗中搜索相关文章：2017高考数学复习：平面向量与复数（四）