2013高考数学复习：圆锥曲线（三）
【方法点拨】
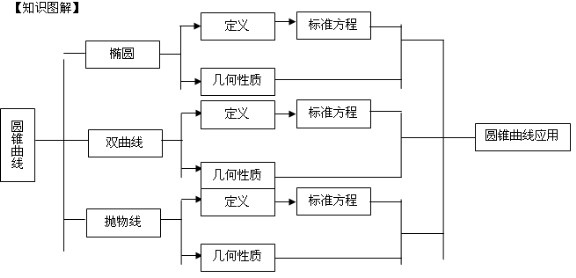
解析几何是高中数学的重要内容之一，也是衔接初等数学和高等数学的纽带。而圆锥曲线是解析几何的重要内容，因而成为高考考查的重点。研究圆锥曲线，无外乎抓住其方程和曲线两大特征。它的方程形式具有代数的特性，而它的图像具有典型的几何特性，因此，它是代数与几何的完美结合。高中阶段所学习和研究的圆锥曲线主要包括三类：椭圆、双曲线和抛物线。圆锥曲线问题的基本特点是解题思路比较简单清晰，解题方法的规律性比较强，但是运算过程往往比较复杂，对学生运算能力，恒等变形能力，数形结合能力及综合运用各种数学知识和方法的能力要求较高。
1. 一要重视定义，这是学好圆锥曲线最重要的思想方法，二要数形结合，既熟练掌握方程组理论，又关注图形的几何性质.
2.着力抓好运算关，提高运算与变形的能力，解析几何问题一般涉及的变量多，计算量大，解决问题的思路分析出来以后，往往因为运算不过关导致半途而废，因此要寻求合理的运算方案，探究简化运算的基本途径与方法，并在克服困难的过程中，增强解决复杂问题的信心，提高运算能力.
3.突出主体内容，要紧紧围绕解析几何的两大任务来学习：一是根据已知条件求曲线方程，其中待定系数法是重要方法，二是通过方程研究圆锥曲线的性质，往往通过数形结合来体现，应引起重视.
4.重视对数学思想如方程思想、函数思想、数形结合思想的归纳提炼，达到优化解题思维、简化解题过程
第3课 双曲线
【考点导读】
1. 了解双曲线的定义、几何图形和标准方程，了解其几何性质
2. 能用双曲线的标准方程和几何性质解决一些简单的实际问题.
【基础练习】
1.双曲线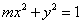
的虚轴长是实轴长的2倍，则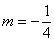
2. 方程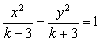
表示双曲线，则
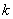的范围是
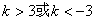
3．已知中心在原点，焦点在y轴的双曲线的渐近线方程为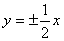
，则此双曲线的离心率为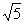
4.已知焦点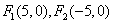
，双曲线上的一点
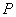到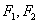
的距离差的绝对值等于
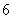，则双曲线的标准方程为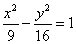
【范例导析】
例1. (1)已知双曲线的焦点在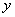
轴上，并且双曲线上两点
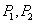坐标分别为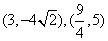
[1] [2] [3] [4] [5] [6] [7] [8] [9] 下一页
- 2017高考数学复习：圆锥曲线（三）
- › 2017马年春节对联：春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章：2017高考数学复习：圆锥曲线（三）
- 在谷歌中搜索相关文章：2017高考数学复习：圆锥曲线（三）
- 在soso中搜索相关文章：2017高考数学复习：圆锥曲线（三）
- 在搜狗中搜索相关文章：2017高考数学复习：圆锥曲线（三）