k)+
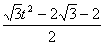 ×(
×(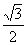 t+k)=0。
t+k)=0。
整理得:t3-3t-4k=0,即k=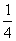 t3-
t3-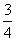 t.
t.
法二:∵a=(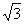 ,-1),b=(
,-1),b=(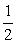 ,
,  ), ∴.
), ∴.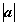 =2,
=2,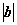 =1且a⊥b
=1且a⊥b
∵x⊥y,∴x·y=0,即-k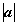 2+t(t2-3)
2+t(t2-3)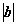 2=0,∴t3-3t-4k=0,即k=
2=0,∴t3-3t-4k=0,即k=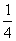 t3-
t3- t
t
(2)由(1)知:k=f(t) =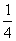 t3-
t3- t ∴k´=f´(t) =
t ∴k´=f´(t) =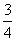 t2-
t2- ,
,
令k´<0得-1<t<1;令k´>0得t<-1或t>1.
故k=f(t)的单调递减区间是(-1,1 ),单调递增区间是(-∞,-1)和(1,+∞).
点拨:第1问中两种解法是解决向量垂直的两种常见的方法:一是先利用向量的坐标运算分别求得两个向量的坐标,再利用向量垂直的充要条件;二是直接利用向量的垂直的充要条件,其过程要用到向量的数量积公式及求模公式,达到同样的求解目的(但运算过程大大简化,值得注意)。第2问中求函数的极值运用的是求导的方法,这是新旧知识交汇点处的综合运用。
例2.已知两个力(单位:牛)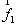 与
与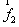 的夹角为
的夹角为 ,其中
,其中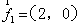 ,某质点在这两个力的共同作用下,由点
,某质点在这两个力的共同作用下,由点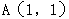 移动到点
移动到点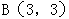 (单位:米)
(单位:米)
(1) 求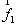
- 2017高考数学复习:平面向量与复数(四)
- › 2017马年春节对联:春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章:2017高考数学复习:平面向量与复数(四)
- 在谷歌中搜索相关文章:2017高考数学复习:平面向量与复数(四)
- 在soso中搜索相关文章:2017高考数学复习:平面向量与复数(四)
- 在搜狗中搜索相关文章:2017高考数学复习:平面向量与复数(四)
