,导函数
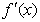 在
在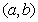 内的图象如图所示,则函数
内的图象如图所示,则函数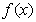 在开区间
在开区间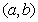 内有极小值点 个
内有极小值点 个
7.统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
8.已知a>0,函数f(x)=lnx-ax2,x>0 (1)求f(x)的单调区间;
(2)当a=时,证明:存在x0∈(2,+∞),使f(x0)=f;
作业(17)
1.设函数f(x)=
A.x=
C.x=2为 f(x)的极大值点 D.x=2为 f(x)的极小值点
2.函数y=
(A)(
3.曲线y=x(3lnx+1)在点
4.曲线y=x3在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为 .
5.设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为
6.若a>0,b>0,函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于
7.设定义在(0,+
(2)若曲线 上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] 下一页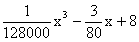 (0
(0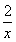 +lnx 则 ( )
+lnx 则 ( )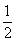 为f(x)的极大值点 B.x=
为f(x)的极大值点 B.x=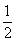 为f(x)的极小值点
为f(x)的极小值点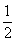 x2
x2 ㏑x的单调递减区间为 ( )
㏑x的单调递减区间为 ( ) 1,1] (B)(0,1] (C.)[1,+∞) (D)(0,+∞)
1,1] (B)(0,1] (C.)[1,+∞) (D)(0,+∞)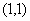 处的切线方程为
处的切线方程为 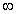 )上的函数
)上的函数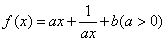 (1)求
(1)求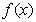 的最小值;
的最小值; 在点
在点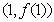
你可能还感兴趣的《高二上册数学(文科)寒假作业及答案》相关文章
