=-4a-b,
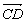 =-5a-3b,其中a、b不共线,则四边形ABCD为梯形
=-5a-3b,其中a、b不共线,则四边形ABCD为梯形
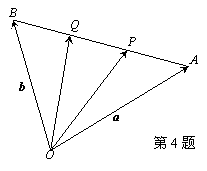
4.如图,设点P、Q是线段AB的三等分点,
若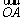 =a,
=a,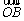 =b,则
=b,则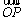 =
= ,
,
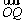 =
=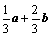 (用a、b表示)
(用a、b表示)
【范例导析】
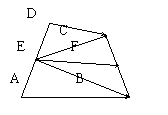
例1 .已知任意四边形ABCD的边AD和BC的中点分别为E、F,
求证: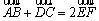 .
.
分析:构造三角形,利用向量的三角形法则证明.
证明:如图,连接EB和EC ,
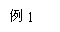 由
由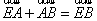 和
和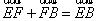 可得,
可得,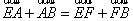 (1)
(1)
由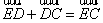 和
和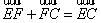 可得,
可得,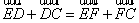 (2)
(2)
(1)+(2)得,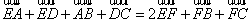 (3)
(3)
∵E、F分别为AD和BC的中点,∴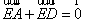 ,
,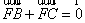 ,
,
代入(3)式得,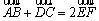
点拨:运用向量加减法解决几何问题时,需要发现或构造三角形或平行四边形.
例2.已知 不共线,
不共线,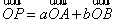 ,求证:A,P,B三点共线的充要条件是
,求证:A,P,B三点共线的充要条件是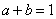
分析:证明三点共线可以通过向量共线来证明.
解:先证必要性:若A,P,B三点共线,则存在实数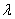
- 2017高考数学复习:平面向量与复数(一)
- › 2017马年春节对联:春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章:2017高考数学复习:平面向量与复数(一)
- 在谷歌中搜索相关文章:2017高考数学复习:平面向量与复数(一)
- 在soso中搜索相关文章:2017高考数学复习:平面向量与复数(一)
- 在搜狗中搜索相关文章:2017高考数学复习:平面向量与复数(一)
