毕节市初三上册数学期末试卷及答案

毕节市初三上册数学期末试卷及答案,标签：中考试题大全,http://www.kuaixue5.com

　　解答：（1）证明：∵DE⊥AC，DF⊥AB，

　　　　　 　∴∠BFD=∠CED=90°，

　　　　　 　又∵BD=CD，BF=CE，

　　　　　 　∴Rt△BDF≌Rt△CDE（HL），

　　　　　 　∴∠B=∠C．

　　　　　 　故△ABC是等腰三角形；（3分）　

（2）解：四边形AFDE是正方形．

　　证明：∵∠A=90°，DE⊥AC，DF⊥AB，

　　　　　∴四边形AFDE是矩形，

　　　　　又∵Rt△BDF≌Rt△CDE，

　　　　　∴DF=DE，

　　　　　∴四边形AFDE是正方形．（8分）

　　点评：此题主要考查学生对等腰三角形的判定及正方形的判定方法的掌握情况．

　　24．考点：一元二次方程的应用．

　　分析：设其中一个正方形的边长为xcm，根据将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．要使这两个正方形的面积之和等于17cm²，可列方程求解．

　　解答：解：设其中一个正方形的边长为xcm，则另一个正方形的边长为．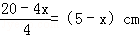

　　依题意列方程得：x²+（5﹣x）²=17，

　　解方程得：x₁=1，x₂=4，

　　答：这两个小正方形的边长分别是1cm、4cm．

　　点评：本题考查理解题意的能力，设出一个正方形的边长，表示出另一个，以面积相等做为等量关系列方程求解．

　　25．考点：反比例函数综合题．

　　专题：计算题；综合题；数形结合．

　　分析：（1）欲求这两个函数的解析式，关键求k值．根据反比例函数性质，k绝对值为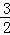且为负数，由此即可求出k；

　　（2）交点A、C的坐标是方程组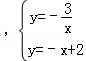的解，解之即得；

　　（3）从图形上可看出△AOC的面积为两小三角形面积之和，根据三角形的面积公式即可求出．

　　解答：解：（1）设A点坐标为（x，y），且x＜0，y＞0，

　　　　则S△ABO=•|BO|•|BA|=•（﹣x）•y=，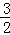

　　　　∴xy=﹣3，

　　　　又∵y=，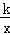

　　　　即xy=k，

　　　　∴k=﹣3．

　　　　∴所求的两个函数的解析式分别为y=﹣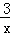，y=﹣x+2；　

　　（2）由y=﹣x+2，

　　　　令x=0，得y=2．

　　　　∴直线y=﹣x+2与y轴的交点D的坐标为（0，2），

　　　　A、C两点坐标满足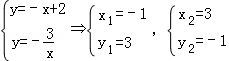

　　　　∴交点A为（﹣1，3），C为（3，﹣1），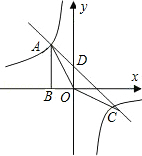

　　　　∴S△AOC=S△ODA+S△ODC=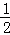OD•（|x₁|+|x₂|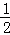）=×2×（3+1）=4．

　　点评：此题首先利用待定系数法确定函数解析式，然后利用解方程组来确定图象的交点坐标，及利用坐标求出线段和图形的面积．

上一页  [1] [2] [3] [4] [5] [6] 

上一篇：青岛版初三上册数学期末试卷及答案

你可能还感兴趣的《毕节市初三上册数学期末试卷及答案》相关文章

• 毕节市初三上册数学期末试卷及答案
• › 毕节市初三上册数学期末试卷及答案
• 在百度中搜索相关文章：毕节市初三上册数学期末试卷及答案
• 在谷歌中搜索相关文章：毕节市初三上册数学期末试卷及答案
• 在soso中搜索相关文章：毕节市初三上册数学期末试卷及答案
• 在搜狗中搜索相关文章：毕节市初三上册数学期末试卷及答案