C、是一次函数，故本选项错误；
D、是二次函数，故本选项错误．
故选B．
点评：本题主要考查对反比例函数的定义，正比例函数的定义，一次函数的定义，二次函数的定义等知识点的理解和掌握，能根据定义区分各个函数是解此题的关键，题型较好，比较典型．
www.kuaixue5.com10．考点：反比例函数的应用．
专题：应用题．
分析：根据题意有：xy=6；故y与x之间的函数图象为反比例函数，且根据x、y实际意义x、y应＞0，其图象在第一象限，即可得出答案．
解答：解：∵xy=6，
∴y=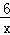
（x＞0，y＞0）．
故选C．
点评：现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．
二、填空题（本大题共10小题，每小题3分，共30分）
11．5考点：直角三角形斜边上的中线；勾股定理．
专题：常规题型．
分析：利用勾股定理求出斜边的长度，然后根据直角三角形斜边上的中线等于斜边的一半的性质解答．
解答：解：根据勾股定理得，斜边=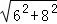
=10cm，
∴斜边上的中线=
×斜边=
×10=5cm．
故答案为：5．
点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理，熟记性质是解题的关键．
12．96考点：菱形的性质．
专题：计算题．
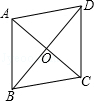
分析：画出草图分析．因为周长是40，所以边长是10．根据对角线互相垂直平分得直角三角形，运用勾股定理求另一条对角线的长，最后根据菱形的面积等于对角线乘积的一半计算求解．
解答：解：因为周长是40cm，所以边长是10cm．
如图所示：AB=10cm，AC=16cm．
根据菱形的性质，AC⊥BD，AO=8cm，
∴BO=6cm，BD=12cm．
∴面积S=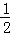
×16×12=96（cm2）．
故答案为96．
点评：此题考查了菱形的性质及其面积计算．主要利用菱形的对角线互相垂直平分及勾股定理来解决．菱形的面积有两种求法：（1）利用底乘以相应底上的高；（2）利用菱形的特殊性，菱形面积=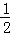×两条对角线的乘积．具体用哪种方法要看已知条件来选择．
13．﹣6考点：待定系数法求反比例函数解析式．.
专题：计算题．
分析：把x=2，y=﹣3代入双曲线解析式即可求得k的值．
解答：解：∵双曲线y=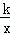
经过点（2，﹣3），
∴k=2×（﹣3）=﹣6，
故答案为﹣6．
点评：考查用待定系数法求反比例函数解析式；用到的知识点为：点在反比例函数解析式上，点的横纵坐标适合函数解析式．
14．6，10，12考点：解一元二次方程-因式分解法；三角形三边关系．
专题：计算题；压轴题．
分析：求△ABC的周长，即是确定等腰三角形的腰与底的长求周长．首先求出方程的根，根据三角形三边关系定理列出不等式，然后解不等式即可．
解答：解：解方程x2﹣6x+8=0得x1=4，x2=2；
当4为腰，2为底时，4﹣2＜4＜4+2，能构成等腰三角形，周长为4+2+4=10；
当2为腰，4为底时4﹣2≠＜2＜4+2不能构成三角形，
当等腰三角形的三边分别都为4，或者都为2时，构成等边三角形，周长分别为6，12，故△ABC的周长是6或10或12．
点评：本题从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．
15．220°考点：多边形内角与外角；等腰三角形的性质．
分析：首先看图，根据等腰三角形的性质可知两个底角的和，然后可得∠1+∠2=360°﹣（两个底角的和），易求解．
解答：解：∵三角形是等腰三角形，
∴两个底角的和为70°×2=140°，
∴∠1+∠2=360°﹣140°=220°．
故答案为：220°．
点评：本题考查了等腰三角形的性质及三角形内角和定理和四边形的内角和为360°等知识．
上一页 [1] [2] [3] [4] [5] [6] 下一页
- 毕节市初三上册数学期末试卷及答案
- › 毕节市初三上册数学期末试卷及答案
- 在百度中搜索相关文章：毕节市初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章：毕节市初三上册数学期末试卷及答案
- 在soso中搜索相关文章：毕节市初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章：毕节市初三上册数学期末试卷及答案