∴AD=BD．
∴△ABD是等腰三角形．
∵AD是角平分线，∠ACB=90°，DE⊥AB，
∴CD=ED∴AC=AE
∴△CDE、△ACE是等腰三角形；
又△CEB也是等腰三角形
显然此图中有4个等腰三角形．
故选C．
点评：本题考查了等腰三角形的判定；要综合运用直角三角形的两个锐角互余和角平分线的性质，找到相等的线段，来判定等腰三角形．
3．考点：简单组合体的三视图．
分析：细心观察图中几何体摆放的位置和形状，根据主视图是从正面看到的图象判定则可．
解答：解：正面看，它是中间小两头大的一个图形，里面有两条虚线，表示看不到的棱．故选B．
点评：本题考查了立体图形的三视图，看得到的棱画实线，看不到的棱画虚线．
4．考点：解一元二次方程-直接开平方法．
分析：首先把﹣5移到方程右边，再两边直接开平方即可．
解答：解：x2﹣5=0，
移项得：x2=5，
两边直接开平方得：x=±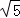
，
则x1=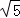，x2=﹣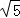
，
故选：D．
点评：此题主要考查了直接开平方法解一元二次方程，解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移项等号的右边，化成x2=a（a≥0）的形式，利用数的开方直接求解．
5．考点：命题与定理．
分析：顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形；既是矩形，又是菱形的四边形是正方形；有一个角是60°的等腰三角形是等边三角形．
解答：解：A、根据菱形的性质和矩形的判定，知正确；
B、根据正方形的判定，知正确；
C、根据正方形的判定，知必须在平行四边形的基础上，故错误；
D、根据等边三角形的判定，知正确．
故选C．
点评：本题考查了特殊四边形的判定、等边三角形的判定．
6．考点：视点、视角和盲区．
分析：电影院呈阶梯或下坡形状可以使后面的观众看到前面，避免盲区．
解答：解：电影院呈阶梯或下坡形状是为了然后面的观众有更大的视角范围，减小盲区．故选B．
点评：本题是结合实际问题来考查学生对视点，视角和盲区的理解能力．
7．考点：中心对称图形；轴对称图形．
专题：几何图形问题．
分析：根据轴对称图形与中心对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
解答：解：A、矩形是轴对称图形，也是中心对称图形，故本选项正确；
B、平行四边形不是轴对称图形，是中心对称图形，故本选项错误；
C、正三角形是轴对称图形，不是中心对称图形，故本选项错误；
D、等腰梯形是轴对称图形，不是中心对称图形，故本选项错误．
故选A．
点评：考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
8．考点：平行投影．
专题：压轴题．
分析：北半球而言，从早晨到傍晚影子的指向是：西﹣西北﹣北﹣东北﹣东，影长由长变短，再变长．
解答：解：根据题意，太阳是从东方升起，故影子指向的方向为西方．然后依次为西北﹣北﹣东北﹣东，故分析可得：先后顺序为④①③②．故选B．
点评：本题考查平行投影的特点和规律．在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，就北半球而言，从早晨到傍晚影子的指向是：西﹣西北﹣北﹣东北﹣东，影长由长变短，再变长．
9．考点：反比例函数的定义；一次函数的定义；正比例函数的定义；二次函数的定义．
专题：推理填空题．
分析：根据反比例函数的解析式是y=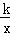
（k是常数，k≠0），A是正比例函数；B、k=
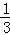，是反比例函数；C、是一次函数；D、是二次函数，即可得到答案．
解答：解：反比例函数的解析式是y=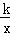（k是常数，k≠0），
A、是正比例函数，故本选项错误；
B、k=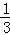，故本选项正确；
上一页 [1] [2] [3] [4] [5] [6] 下一页
- 毕节市初三上册数学期末试卷及答案
- › 毕节市初三上册数学期末试卷及答案
- 在百度中搜索相关文章：毕节市初三上册数学期末试卷及答案
- 在谷歌中搜索相关文章：毕节市初三上册数学期末试卷及答案
- 在soso中搜索相关文章：毕节市初三上册数学期末试卷及答案
- 在搜狗中搜索相关文章：毕节市初三上册数学期末试卷及答案