初三数学切线长定理例题解析
(直线与圆的位置关系)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
【证明】∵ PA , PB 与⊙ O 相切,点 A , B 是切点,∴ OA ⊥ PA , OB ⊥ PB 即∠ OAP= ∠ OBP=90 °,∵ OA=OB , OP=OP ,∴ Rt △ AOP ≌ Rt △ BOP(HL) ,∴ PA = PB ,∠ OPA= ∠ OPB 。
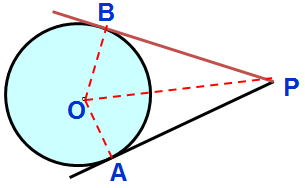
切线 6 个性质:
1 、切线和圆只有一个公共点;
2 、切线和圆心的距离等于圆的半径;
3 、切线垂直于过切点的半径;
4 、经过圆心垂直于切线的直线必过切点;
5 、经过切点垂直于切线的直线必过圆心。
6 、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
【内切圆计算练习题】
1 、一个三角形有且只有一个内切圆;
2 、一个圆有无数个外切三角形;
3 、三角形的内心就是三角形三条内角平分线的交点;
4 、三角形的内心到三角形三边的距离相等。
【例 1 】 △ ABC 的内切圆⊙ O 与 BC 、 CA 、 AB 分别相切于点 D 、 E 、 F ,且 AB=225px , BC=350px , CA=325px ,求 AF 、 BD 、 CE 的长 .
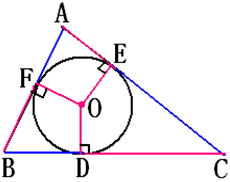
【解答】∵⊙ O 与△ ABC 的三边都相切,∴ AF = AE,BD = BF,CE = CD ,设 AF=x , BD=y , CE = z ,则 x + y = 9 , y + z = 14 , x + z = 13 ,解得 x=4 , y=5 , z=9 。

【例 2 】 △ ABC 的内切圆的半径为 r ,△ ABC 的周长为 l ,求△ ABC 的面积 S.
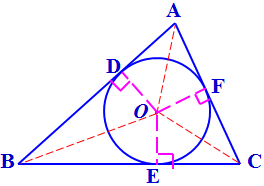
【解答】设△ ABC 的内切圆与三边相切于 D 、 E 、 F ,连结 OA 、 OB 、 OC 、 OD 、 OE 、 OF ,则 OD ⊥ AB , OE ⊥ BC , OF ⊥ AC 。∴ S △ ABC = S △ AOB + S △ BOC + S △ AOC = (AB · OD)/2 + (BC · OE)/2 + (AC · OF)/2=(l · r)/2 ,设△ ABC 的三边为 a 、 b 、 c ,面积为 S ,则△ ABC 的内切圆的半径 r = 2S/( a+b+c ) 。
【例 3 】 Rt △ ABC 中,∠ C = 90 °, BC = a , AC = b , AB = c ,⊙ O 为 Rt △ ABC 的内切圆。 求: Rt △ ABC 的内切圆的半径 r.
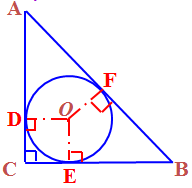
【解答】设 Rt △ ABC 的内切圆与三边相切于 D 、 E 、 F ,连结 OD 、 OE 、 OF 则 OA ⊥ AC , OE ⊥ BC , OF ⊥ AB 。∵⊙ O 与 Rt △ ABC 的三边都相切,∴ AD = AF , BE = BF , CE = CD ,设 AD= x , BE= y , CE = r ,则有 x + r = b , y + r = a , x + y = c ,解得 r=( a+b-c )/2 或 r= ab /( a+b+c ) 。
【例 4 】 Rt △ ABC 中,∠ C = 90 ° ,BC = 3,AC = 4, ⊙ O 为 Rt △ ABC 的内切圆 . ( 1 )求 Rt △ ABC 的内切圆的半径;( 2 )若移动点 O 的位置,使⊙ O 保持与△ ABC 的边 AC 、 BC 都相切,求⊙ O 的半径 r 的取值范围。

- 初三数学切线长定理例题解析
- › 新初三数学应如何预习?
- › 初三数学抓好课前、课中、课后
- › 初三数学期末考试复习技巧
- › 初三数学期末考试复习方法及技巧
- › 初三数学期末考试复习计划:保持良好心态
- › 初三数学期末考试复习计划:重视复习策略
- › 初三数学复习四大原则需记牢
- › 初三数学五种错误如何逐个突破
- › 中考复习指导:初三数学复习计划
- › 北京昌平区初三数学上册期末考试卷
- › 黄石2016年初三数学上册期末试题及答案
- › 大丰实验初中初三数学期末试卷及答案
- 在百度中搜索相关文章:初三数学切线长定理例题解析
- 在谷歌中搜索相关文章:初三数学切线长定理例题解析
- 在soso中搜索相关文章:初三数学切线长定理例题解析
- 在搜狗中搜索相关文章:初三数学切线长定理例题解析
