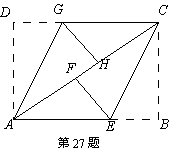
(1)试说明四边形AECG是平行四边形;
(2)若矩形的一边AB的长为3cm,当BC的长为多少时,四边形AECG是菱形?
28.(本题满分6分)
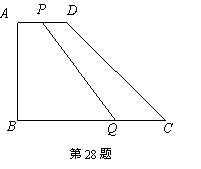
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动. 当Q点到达B点时,动点P、Q同时停止运动. 设点P、Q同时出发,并运动了t秒,
(1)直角梯形ABCD的面积为 cm2.
(2)当t= 秒时,四边形PQCD成为平行四边形?
(3)当t= 秒时,AQ=DC;
(4)是否存在t,使得P点在线段DC上且PQ⊥DC?若存在,求出此时t的值,若不存在,说明理由.
www.kuaixue5.com
八年级数学期终试卷参考答案及评分标准
一、细心填一填
1.;;-8 2.;; 3.2 4.38,3 5.40 6.135 7.15 8.6 9.150 10.6 11.或 12.160 13.(1)24 (2)96 (3)(或填)
二、精心选一选
14.B 15.D 16.D 17.D 18.B 19.A 20.C
三、认真答一答
21.(1)原式=(2分)=-1(3分)
(2)原式=(2分)=(3分)
(3)原式=(2分)=(3分)
当,y=-3时,原式=-6+90=84(4分)
22.(1)原式=(2分)=(3分)
(2)原式=(1分)=(2分)
=(3分)
23.(1)(2分) (2)略(4分)
24.(1)AB=,AC=,BC=(1分,不化简也对)
∴∴△ABC是Rt△(2分)
(2)图略(3分) (3)图略(4分)(写出等式与画图各1分,图上不标线段长不得分)
(4)先将△A2B2C2绕A2点按顺时针方向旋转90°,再将所得图形向右平移6个单位即得到△A1B1C1(5分,变换可以不同,只要正确即可)
25.证明:(1)连结AC交BD于O.(1分)
∵ABCD是平行四边形,∴OA=OC,OB=OD,(2分)
∵BE=DF∴OE=OF ∴四边形AECF的平行四边形(3分)
(2)∵四边形AECF的平行四边形 ∴AF∥EC ∴∠FAC=∠ECA (4分)
∵ABCD是平行四边形 AD∥BC ∴∠DAC=∠BCA ∴∠DAF=∠BCE (5分)
26.(1)解:∵△ABC沿AB方向平移AB长得到△BDE ∴AB=CE=BD,BC=DE,(1分)
∵AB=BC ∴BD=DE=CE=BC,(2分)∴四边形BDEC为菱形.(3分)
(2)证明:∵四边形BDEC为菱形 ∴BE⊥CD(4分) ∵△ABC沿AB方向平移AB长得到△BDE ∴AC∥BE ∴AC⊥CD.(5分)
27.(1)由题意,得∠GAH=∠DAC, ∠ECF=∠BCA(1分)
∵四边形ABCD为矩形 ∴AD∥BC ∴∠DAC=∠BCA∴∠GAH=∠ECF∴AG∥CE(2分)
又∵AE∥CG ∴四边形AECG是平行四边形(3分)
(2)∵四边形AECG是菱形 ∴F、H重合∴AC=2BC(4分)
在Rt△ABC中,设BC=x,则AC=2x 在Rt△ABC中
即,解得x=,即线段BC的长为cm.(5分)
28.解:(1)48(1分) (2)秒(2分) (3)0.8秒(3分)
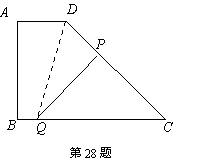
(4)如图,设QC=5t,则DP=4t-4,∵CD=10 ∴PC=14-4t,连结DQ,
∵AB=6,∴
若PQ⊥CD,则
∴5PQ=15t, 即PQ=3t (4分)
∵PQ⊥CD 则QC2=PQ2+PC2 ∴
解得t=(5分)
当t=时,4<4t<14,此时点P在线段DC上,又5t=<12 点Q在线段CB上.
∴当P点运动到DC上时,存在t=秒,使得PQ⊥CD.(6分)
- 初二上册数学期末综合复习试题及答案
- › 镇江外国语学校初二上册英语期末试卷及答案
- › 四川眉山初二上册数学期末试题及答案
- › 初二上册数学期末试题及答案
- › 初二上册数学期末试卷及答案汇总
- › 2016初二上册数学期末冲关训练4
- › 2016初二上册数学期末冲关训练3
- › 2016初二上册数学期末冲关训练2
- › 2016初二上册数学期末冲关训练1
- › 南通海门初二上册数学期末试卷
- › 宿迁实验初中初二上册数学期末质量检测
- › 瓜州二中初二上册数学期末试卷及答案
- › 初二上册数学期末模拟试题及答案
- 在百度中搜索相关文章:初二上册数学期末综合复习试题及答案
- 在谷歌中搜索相关文章:初二上册数学期末综合复习试题及答案
- 在soso中搜索相关文章:初二上册数学期末综合复习试题及答案
- 在搜狗中搜索相关文章:初二上册数学期末综合复习试题及答案
