求证:AB∥平面EFG.
证明 :∵面EFGH是截面.
∴点E,F,G,H分别在BC,BD,DA,AC上.
∴EH  面ABC,GF
面ABC,GF  面ABD,
面ABD,
由已知,EH∥GF.∴EH∥面ABD.
又 ∵EH  面BAC,面ABC∩面ABD=AB
面BAC,面ABC∩面ABD=AB
∴EH∥AB.
∴AB∥面EFG.
例2. 如图,在正方体ABCD—A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.
求证:MN∥平面AA1B1B.
分析:“线线平行”、“线面平行”、“面面平行”是可以互相转化的。本题可以采用任何一种转化方式。
简证:法1:把证“线面平行”转化为证“线线平行”。
即在平面ABB1A1内找一条直线与MN平行,如图所示作平行线即可。
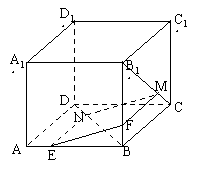
法2:把证“线面平行”转化为证“线线平行”。连CN并延长交直线BA于点P,
连B1P,就是所找直线,然后再设法证明MN∥B1P.
法3:把证“线面平行”转化为证“面面平行”。
过M作MQ//BB1交BC于B1,连NQ,则平面MNQ与平面ABB1A1平行,
从而证得MN∥平面ABB1A1.
点评:证明线面或面面平行的时候一定要注意相互的转化,非常灵活。
【反馈演练】
1.对于平面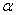 和共面的直线
和共面的直线 、
、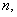 下列命题中真命题是(3)。
下列命题中真命题是(3)。
(1)若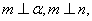 则
则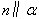 (2)若
(2)若 则
则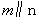
(3)若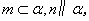 则
则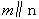 (4)若
(4)若 、
、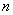 与
与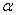 所成的角相等,则
所成的角相等,则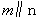
2. 设a、b是两条异面直线,那么下列四个命题中的假命题是 (2) 。
(1)经过直线a有且只有一个平面平行于直线b
(2)经过直线a有且只有一个平面垂直于直线b
(3)存在分别经过直线a和b的两个互相平行的平面
(4)存在分别经过直线a和b的两个互相垂直的平面
3.关于直线a、b、l及平面M、N,下列命题中正确的是(4) 。
(1)若a∥M,b∥M,则a∥b (2)若a∥M,b⊥a,则b⊥M
(3)若a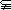
- 2017高考数学复习:立体几何初步(三)
- › 2017马年春节对联:春节七字春联齐齐看
- › 2017年感恩节是几月几日
- › 2017年中秋节活动方案
- › 2017中秋节活动方案汇总
- › 2017中秋节活动方案
- › 2017麓山国际实验学校新高一入学安排
- › 2017明德中学秋季高一新生入学须知
- › 2017长沙市实验中学高中新生入学安排
- › 2017广益实验中学高一新生入学须知
- › 2017长郡湘府班高一新学生报到须知
- › 2017长郡中学高一新生报到须知
- › 2017雅礼中学高中新生入学须知
- 在百度中搜索相关文章:2017高考数学复习:立体几何初步(三)
- 在谷歌中搜索相关文章:2017高考数学复习:立体几何初步(三)
- 在soso中搜索相关文章:2017高考数学复习:立体几何初步(三)
- 在搜狗中搜索相关文章:2017高考数学复习:立体几何初步(三)
