兰州一中高二上册数学期末试卷及答案
一、选择题:(本大题共12小题,每小题3分,共36分,在每个小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填在试卷的答题卡中.)
1.若抛物线y2=2px的焦点与椭圆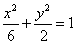 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )
A.-2 B.2 C.-4 D.4
2.(理)已知向量a=(3,5,-1),b=(2,2,3),c=(4,-1,-3),则向量2a-3b+4c的坐标为( )
A.(16,0,-23) B.(28,0,-23) C.(16,-4,-1) D.(0,0,9)
(文)曲线y=4x-x2上两点A(4,0),B(2,4),若曲线上一点P处的切线恰好平行于弦AB,则点P的坐标为( )
A.(1,3) B.(3,3) C.(6,-12) D.(2,4)
3.过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
A.1条 B.2条 C.3条 D.4条
4.已知双曲线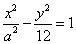 的离心率2,则该双曲线的实轴长为( )
的离心率2,则该双曲线的实轴长为( )
A.2 B.4 C.2 D.4
D.4
5.在极坐标系下,已知圆C的方程为r=2cosθ,则下列各点中,在圆C上的是( )
A.(1,-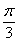 ) B.(1,
) B.(1,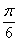 ) C.(
) C.(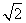 ,
, ) D.(
) D.(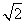 ,
, )
)
6.将曲线y=sin3x变为y=2sinx的伸缩变换是( )
A.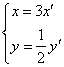 B.
B.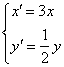 C.
C. D.
D.
7.在方程 (q为参数)表示的曲线上的一个点的坐标是( )
(q为参数)表示的曲线上的一个点的坐标是( )
A.(2,-7) B.(1,0) C.(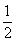 ,
,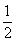 ) D.(
) D.(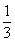 ,
,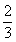 )
)
8.极坐标方程r=2sinq和参数方程 (t为参数)所表示的图形分别为( )
(t为参数)所表示的图形分别为( )
A.圆,圆 B.圆,直线 C.直线,直线 D.直线,圆
9.(理)若向量a=(1,l,2),b=(2,-1,2),a、b夹角的余弦值为 ,则?=( )
,则?=( )
A.2 B.-2 C.-2或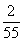 D.2或-
D.2或-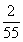
(文)曲线y=ex![]() +x在点(0,1)处的切线方程为( )
+x在点(0,1)处的切线方程为( )
A.y=2x+1 B.y=2x-1 C.y=x+1 D.y=-x+1
10.(理)已知点P1的球坐标是P1(4, ,
, ),P2的柱坐标是P2(2,
),P2的柱坐标是P2(2,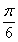 ,1),则|P1P2|=( )
,1),则|P1P2|=( )
A.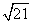 B.
B.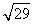 C.
C.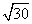 D.
D.
(文)已知点P在曲线f(x)=x4-x上,曲线在点P处的切线垂直于直线x+3y=0,则点P的坐标为( )
A.(0,0) B.(1,1) C.(0,1) D.(1,0)
11.过 双曲线的右焦点F作实轴所在直线的垂线,交双曲线于A,B两点,设双曲线的左顶点M,若点M在以AB为直径的圆的内部,则此双曲线的离心率e的取值范围为( )
双曲线的右焦点F作实轴所在直线的垂线,交双曲线于A,B两点,设双曲线的左顶点M,若点M在以AB为直径的圆的内部,则此双曲线的离心率e的取值范围为( )
A.(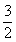 ,+∞) B.(1,
,+∞) B.(1,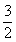 ) C.(2,+∞) D.(1,2)
) C.(2,+∞) D.(1,2)
12.从抛物线y2=4x上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△MPF的面积为( )
A.5 B.10 C.20 D.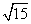
二、填空题:(本大题共4小题,每小题4分,共16分.请将答案填在试卷的答题卡中.)
13.(理)已知空间四边形ABCD中,G是CD的中点,则 = .
= .
(文)抛物线y=x2+bx+c在点(1,2)处的切线与其平行直线bx+y+c=0间的距离是 .
14.在极坐标系中,设P是直线l:r(cosθ+sinθ)=4上任一点,Q是圆C:r2=4rcosθ-3上任一点,则|PQ|的最小值是________.
15.(理)与A(-1,2,3),B(0,0,5)两点距离相等的点P(x,y,z)的坐标满足的条件为__________.
(文)函数f(x)=ax3-x在R上为减函数,则实数a的取值范围是__________.
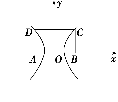 16.如图,已知双曲线以长方形ABCD的顶点A、B为左、右焦点,且双曲线过C、D两顶点.若AB=4,BC=3,则此双曲线的标准方程为____________________.
16.如图,已知双曲线以长方形ABCD的顶点A、B为左、右焦点,且双曲线过C、D两顶点.若AB=4,BC=3,则此双曲线的标准方程为____________________.
三、解答题:(本大题共4小题,共48分,解答应写出文字说明,证明过程或演算步骤.)
17.(本题满分12分)
双曲线与椭圆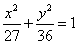 有相同焦点,且经过点(
有相同焦点,且经过点(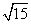 ,4),求其方程.
,4),求其方程.
18.(本题满分12分)
在直角坐标系xOy中,直线l的参数方程为: (t为参数),若以O为极点,x轴正半轴为极
(t为参数),若以O为极点,x轴正半轴为极 轴建立极坐标系,则曲线C的极坐标方程为r=
轴建立极坐标系,则曲线C的极坐标方程为r=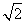 cos(θ+
cos(θ+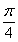 ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长.
19.(本题满分12分)
已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离为5,求抛物线的方程和m的值.
20.(本题满分12分)
(文)已知函数f(x)=x2(x-a).
(1)若f(x)在(2,3)上单调,求实数a的取值范围;
(2)若f(x)在(2,3)上不单调,求实数a的取值范围.
 (理)(本题满分12分)
(理)(本题满分12分)
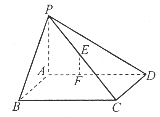
如图,四棱锥P—ABCD的底面是矩形,PA⊥面ABCD,PA=2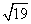 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
(1)求EF的长;
(2)证明:EF⊥PC.
参考答案:
一、选择题:本大题共12小题 ,每小题3分,共36分.
,每小题3分,共36分.

( )内为文科答案
二、填空题:(本大题共4小题,每小题4分,共16 分.)
分.)
13.(理)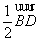 (文)
(文)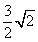 14.
14.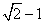
15.(理)2x-4y+4z=11 (文)a≤0 16.x2-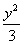 =1
=1
三、解答题:(本大题共4小题,共48分,解答应写出文字说明,证明过程或演算步骤.)
17.(本题满分12分)
解:椭圆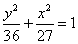 的焦点为(0,±3),c=3,………………………3分
的焦点为(0,±3),c=3,………………………3分
设双曲线方程为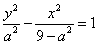 ,…………………………………6分
,…………………………………6分
∵过点(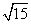 ,4),则
,4),则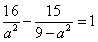 ,……………………………9分
,……………………………9分
得a2=4或36,而a2<9,∴a2=4,………………………………11分
双曲线方程为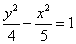 .………………………………………12分
.………………………………………12分
18.(本题满分12分)
解:将方程 (t为参数)化为普通方程得,3x+4y+
(t为参数)化为普通方程得,3x+4y+ 1=0,………3分
1=0,………3分
将方程r=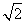 cos(θ+
cos(θ+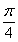 )化为普通方程得,x2+y2-x+y=0, ……………6分
)化为普通方程得,x2+y2-x+y=0, ……………6分
它表示圆心为(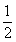 ,-
,-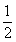 ),半径为
),半径为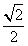 的圆, …………………………9分
的圆, …………………………9分
则圆心到直线的距离d=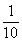 , …………………………………………10分
, …………………………………………10分
弦长为2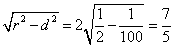 . …………………………………12分
. …………………………………12分

20.(文)(本题满分12分)
解:由f(x)=x3-ax2得f′(x)=3x2-2ax=3x(x- ).…………3分
).…………3分
(1)若f(x)在(2,3)上单调,则 ≤0,或0<
≤0,或0< ≤2,解得:a≤3.…………6分
≤2,解得:a≤3.…………6分
∴实数a的取值范围是(-∞,3].…………8分
(2)若f(x)在(4,6)上不单调,则有4< <6,解得:6
<6,解得:6
∴实数a的取值范围是(6,9).…………12分
 20.(理)(本题满分12分)
20.(理)(本题满分12分)
解:(1)以A为原点,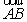 ,
,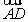 ,
,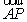 分别为x,y,z轴建立直角坐标系,…………2分
分别为x,y,z轴建立直角坐标系,…………2分
由条件知:AF=2,………… 3分
3分
∴F(0,2,0),P(0,0,2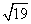 ),C(8,6,0).…4分
),C(8,6,0).…4分
从而E(4,3,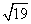 ),∴EF=
),∴EF=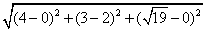 =6.…………6分
=6.…………6分
(2)证明: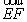 =(-4,-1,-
=(-4,-1,-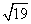 ),
), =(8,6,-2
=(8,6,-2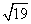 ),…………8分
),…………8分
∵ =-4×8+(-1)×6+(-
=-4×8+(-1)×6+(-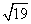 )×(-2
)×(-2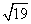 )=0,…………10分
)=0,…………10分
∴EF⊥PC.…………12分
- 兰州一中高二上册数学期末试卷及答案
- › 甘肃兰州一中高二英语试题
- › 兰州一中高二上册英语期末试卷及答案
- › 兰州一中高二上册数学期末试卷及答案
- › 甘肃兰州一中高一英语试题
- › 兰州一中高一上册英语期末试卷及答案
- › 兰州一中高一年级英语期末试题
- › 兰州一中高一数学期末试题及答案
- › 兰州一中高一上册数学期末试卷及答案
- 在百度中搜索相关文章:兰州一中高二上册数学期末试卷及答案
- 在谷歌中搜索相关文章:兰州一中高二上册数学期末试卷及答案
- 在soso中搜索相关文章:兰州一中高二上册数学期末试卷及答案
- 在搜狗中搜索相关文章:兰州一中高二上册数学期末试卷及答案
