试题精选七——抽屉原理

　　例：圆上的100个点将该圆分为100段等弧。随意将其中的一些点染成红点，要保证至少有4个红点是一个正方形的4个顶点。问：你至少要染红多少点？           

　　解：至少要染红76个点。

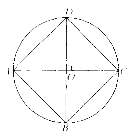
　　如图所示：圆的一对直径AC，BD互相垂直时，则ABCD恰是一个正方形。反过来，如果圆上的四点A，B，C，D恰是正方形ABCD的4个顶点，则对角线AC，BD恰是该圆的一对互相垂直的直径。圆上的100个点将该圆分成100段等弧。恰好25对互相垂直的直径，由互相垂直的直径的4个端点恰好构成25个不同的正方形。最不利的情形是：每对互相垂直的直径的4个端点中染红3个点，则总计在圆的100个等分点中染红了75个点，其中任意4个红点都不是一个正方形的4个 顶点。

　　这时，我们只要再染一个红点，即染76个红点，而，就必须会出现一个正方形的4个顶点都是红点。因此，要保证至少有一个正方形的4个顶点为红点，至少要将这100个等分点中的76个点染成红点。

你可能还感兴趣的《试题精选七——抽屉原理》相关文章

• 试题精选七——抽屉原理
• › 试题精选十三——行程问题
• › 试题精选十四 —— 工程问题（小学组）
• › 试题精选十六——工程问题
• › 试题精选十七—— 奇偶分析
• › 试题精选十八——计算问题
• › 试题精选三——循环数计算
• › 试题精选四——不定方程
• › 试题精选五——勾股定理
• › 试题精选六——内角和
• › 试题精选七——抽屉原理
• › 试题精选二十——代数问题
• › 试题精选一——趣味思考题
• 在百度中搜索相关文章：试题精选七——抽屉原理
• 在谷歌中搜索相关文章：试题精选七——抽屉原理
• 在soso中搜索相关文章：试题精选七——抽屉原理
• 在搜狗中搜索相关文章：试题精选七——抽屉原理