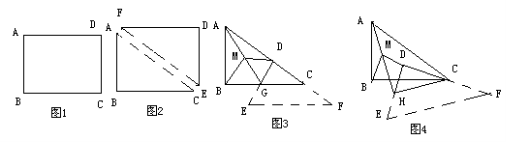
23.小华将一张矩形纸片（如图1）沿对角线AC剪开，得到两张三角形纸片（如图2），其中∠ACB＝β，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上。
（1）若DE与BC相交于点G，取AG的中点M，连结MB，MD，当△EFD纸片沿CA方向平移时（如图3），请你猜想并写出MB与MD的数量关系，然后证明你的猜想；（3分）
（2）在（1）的条件下，求出∠BMD的大小（用含β的式子表示），并说明当β＝45o时，△BMD是什么三角形；（5分）
（3）在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度（小于90o），此时△CGD变成△CHD，同样取AH的中点M，连结MB，MD（如图4），请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不证明，并说明β为何值时△BMD为等边三角形。（2分）
26. （本小题满分10分）问题背景：在△ABC中，AB、BC、AC三边的长分别为√5、√10、√13，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处)，如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
(1)请你将△ABC的面积直接填写在横线上:______________．
思维拓展：(2)我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别为a、2a、a(a＞0)，请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积．
探索创新：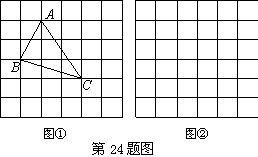
(3)若△ABC三边的长分别为√(m2+16n2)、√(9m2+4n2)、2√(m2+n2)(m＞0，n＞0，且m≠n)，试运用构图法求出这三角形的面积．
- 八年级期中经典练习题
- › 八年级期中经典练习题
- 在百度中搜索相关文章：八年级期中经典练习题
- 在谷歌中搜索相关文章：八年级期中经典练习题
- 在soso中搜索相关文章：八年级期中经典练习题
- 在搜狗中搜索相关文章：八年级期中经典练习题